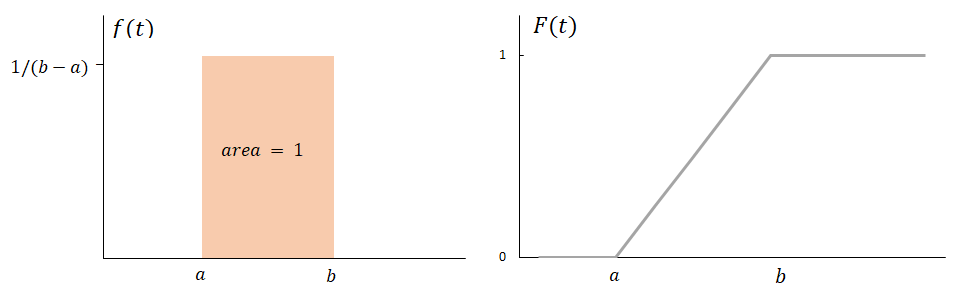
Exhibit 34.15 Uniform probability distribution.
Uniform distribution, or rectangular distribution, is a distribution that has constant
probability over a fixed range. A random variable, X, is uniform on [a,b] if
X is equally likely to take any value in the range from a to b
(Exhibit 34.15).
Notation: [a, b] means continuous values from a to b.
$$X∼U[a,b]$$
$$f(t)=\begin{cases}\frac{1}{b-a}, \,\,if \,\,a \, \le t \le b \\ \\0 \,otherwise \end{cases}$$
The cumulative distribution function (cdf):
$$F(t)=\begin{cases}0 \,\,if \,\,t< a \\ \\ \frac{t-a}{b-a} \,\,if \,\,a \le t \le b \\ \\ 1 \,\,if \,\,t>b \end{cases}$$
$$E(X)= \frac{b-a}{2}, \,Var(X)=\frac{b-a}{12}$$