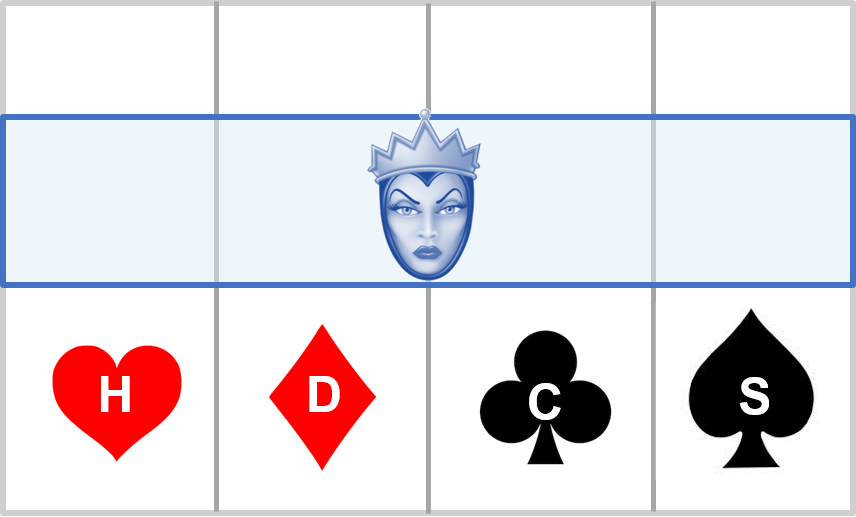
Exhibit 34.5 The events H (heart), D, C and S are mutually
exclusive and collectively exhaustive.
The law of total probability is a rule relating marginal probabilities to conditional
probabilities. It expresses the total probability of an outcome which can be realized via several
distinct events.
Consider n mutually exclusive and collectively exhaustive events, A1,
A2 … An, the probability for any event B to occur:
$$P(B)=\sum_{i=1}^n P(B∩A_i )=P(B∩A_1 )+P(B∩A_2 )… P(B∩A_n)$$
$$P(B)=P(B│A_1 )P(A_1 )+P(B│A_2 )P(A_2 )… P(B|A_n)P(A_n)$$
Taking cards for example (Exhibit 34.5), the probability of picking a queen:
$$P(Q)=P(Q│H)P(H)+P(Q│D)P(D)+P(Q|C)P(C)+P(Q|S)P(S)$$
Basically, this is the same as weighted average.
Example: As shown is Exhibit 34.6, the age profile of a target population
(universe) is broken down into 4 groups: below 20, 20 to 30, 30 to 50 and over 50. The proportion of the
population that falls in each group is 20%, 20%, 40% and 20% respectively, and the proportion of brand
buyers in each is 10%, 15%, 20% and 15%. Based on this information, the proportion of brand buyers in the
target population is 16%, as computed in Exhibit 34.6.
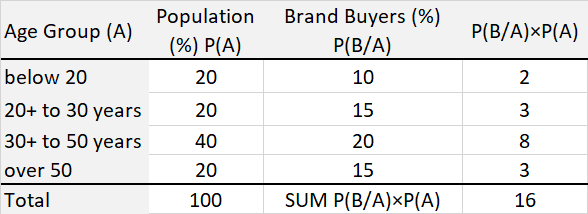
Exhibit 34.6 Computing the weighted average brand buyers.