Two-tailed tests with known mean and standard deviation also use the
z-score statistic. In such cases, the z-score can be used in conjunction with the normal
distribution, provided that the population’s standard deviation is known.
Example: The mean weight of fresh recruits into the army was reported
to be 65.8 kg last year. This year, a sample of 200 recruits was taken, and the mean weight was
found to be 66.2 kg. Assuming the population standard deviation is 3.2 kg, at 0.05
significance level, can we conclude that the mean weight has changed since last year?
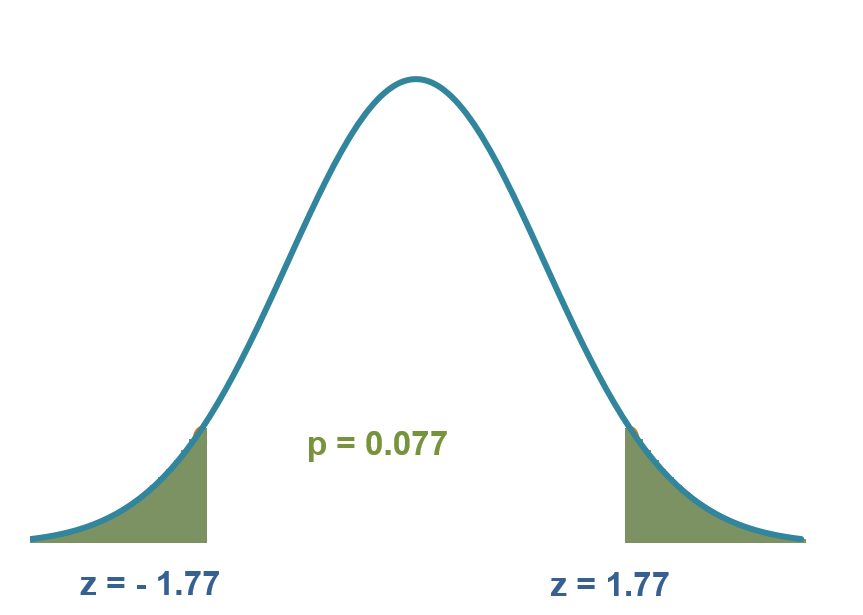
Exhibit 34.22 If the actual mean was 65.8 kg, there is a 7.7% probability that the sampled recruits would
weigh ≥ 66.2 kg or ≤ 65.4 kg.
H0: μ=65.8
HA: μ≠65.8
α = 5%
$$ z = \frac{\bar x-μ}{s/\sqrt n} = \frac{66.2-65.8}{3.2/14.14} = 1.77 $$
p-value = 0.077 > α = 0.05
The p-value of 0.077 (7.7%), obtained from normal distribution (Exhibit 34.22) for z = 1.77, is not significant for
the given level of 5%.
If the actual mean was 65.8 kg, there is a 7.7% probability that the sampled recruits would weigh ≥ 66.2 kg
or ≤ 65.4 kg. Since this probability is higher than the significance level of 5%, the null hypothesis is not rejected. We cannot
conclude with 95% certainty that the new recruits differ in weight from those recruited last year.