Probability Theory

Quantitative research relies on probability theory to analyse and interpret data, make predictions, and draw meaningful conclusions. This introduction aims to provide an overview, covering essential terms and concepts within the realm of probability theory in the context of marketing analytics and quantitative research.

Objective and Subjective

In general, probabilities can be classified into two types: objective probabilities and subjective probabilities:

• Objective probabilities that can be estimated from proportions, based on empirical data. For instance, P(Q), or for instance, the probability that a retail store is handling the brand Coca-Cola.
• Subjective probabilities that cannot be estimated from long-run proportions. For example, an applicant feels she has a 50% chance of getting a job. This is her opinion, and it is subjective.

Terms and Concepts

A random variable is a variable whose possible values are numerical outcomes of a probabilistic experiment. It can either be discrete, taking a finite set of numeric values, or continuous, in which case the range of values is infinite.

Probability is the likelihood that an event will occur. It varies between 0 and 1, where 0 indicates impossibility and 1 indicates certainty. The higher the probability, the more likely that the event will occur.

Probability is defined in the context of a sample space or universe, i.e., a set of all possible outcomes. For instance, the universe of stores in retail tracking, is all the stores that represent the “total market” measured by the tracking service.

As an example, consider pack of cards. The universe constitutes the 52 cards shown in Exhibit 34.1. If you pick a card at random, the probability it will be a queen, P(Q), is 4/52, and the probability it will be the queen of hearts, P(Q_hearts) is 1/52.

The complement of an event, Q, is the probability that the event will not occur. It is denoted by: Q̄: P(Q̄)=1−P(Q).

The probability that the card you pick is not a queen, is 1 – P(Q) = 48/52.

Mutually Exclusive Events and Overlapping Events

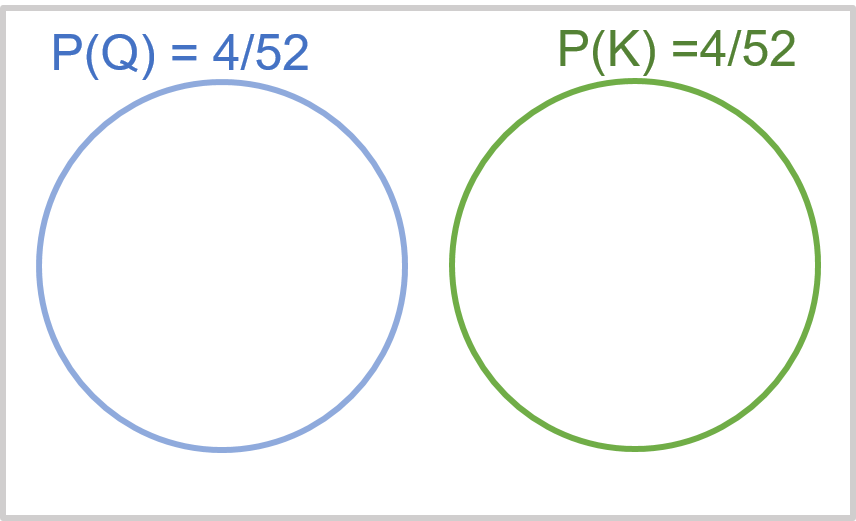
As shown in Exhibit 34.3, the events picking a queen (Q) and picking a king (K) are mutually exclusive; their range of possible values do not overlap. For such mutually exclusive events, the probability that either one or the other will occur, is a summation of their individual probabilities:

$$P(Q \,or \,K) = P(Q) + P(K)$$

The probability that the card is either a queen or a king is 4/52 + 4/52 = 8/52.

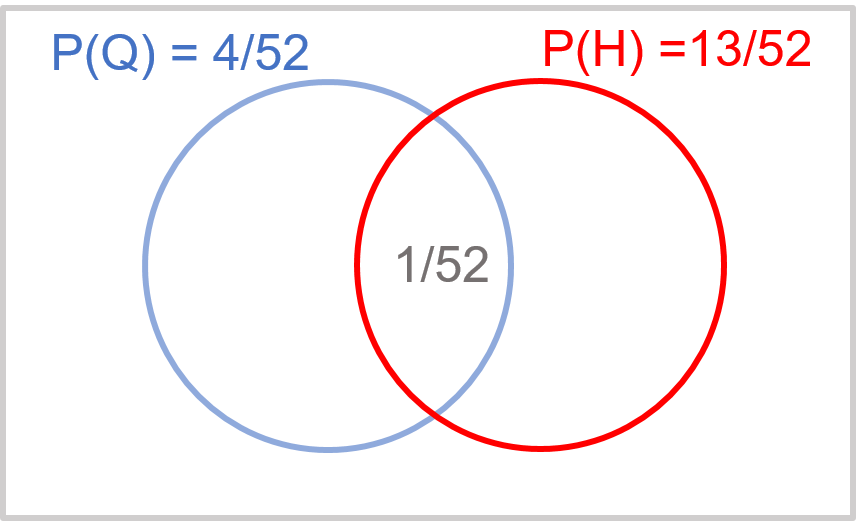
If Q and H are not mutually exclusive events, their range of possible values will overlap as shown in Exhibit 34.4, and the probability that either will occur is:

$$P(Q \,or \,H) = P(Q) + P(H) - P (Q \,and \,H)$$

The probability that the card is either a queen or a heart is 4/52 + 13/52 – 1/52.

Conditional (Posterior) Probability

Conditional Probability is the probability of an event given that another event has already occurred. For instance, probability that the card is a queen, given it is a heart.

$$P(Q|H) = \text{probability that Q will occur, given H has occurred.}$$ $$P(Q│H)=(P(Q∩H))/(P(H))=(1/52)/(13/52)$$

This implies:

$$P(Q∩H)=P(Q│H)×P(H)=P(H│Q)×P(Q)$$

Independent Events

Events are independent if knowing whether one has occurred does not change the probability of the other.

Suppose you pick a card and toss a coin. The probability of getting a tail, P(T), in no way influences the probability of getting a queen, P(Q), from a pack of cards.

$$P(T│Q)=P(T),\,and \,P(Q│T)=P(Q)$$ $$P(T∩Q)=P(T)×P(Q)$$

Law of Total Probabilities

The law of total probability is a rule relating marginal probabilities to conditional probabilities. It expresses the total probability of an outcome which can be realized via several distinct events.

Consider n mutually exclusive and collectively exhaustive events, A₁, A₂ … A_n, the probability for any event B to occur:

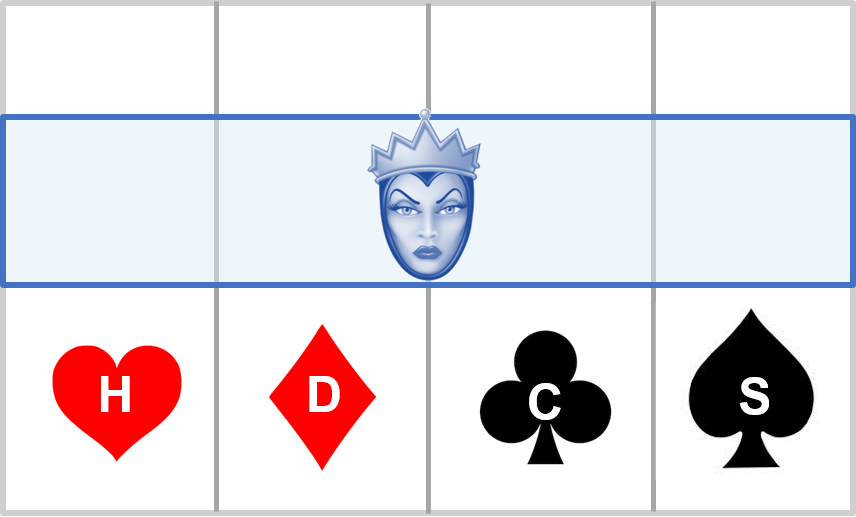
$$P(B)=\sum_{i=1}^n P(B∩A_i )=P(B∩A_1 )+P(B∩A_2 )… P(B∩A_n)$$ $$P(B)=P(B│A_1 )P(A_1 )+P(B│A_2 )P(A_2 )… P(B|A_n)P(A_n)$$

Taking cards for example (Exhibit 34.5), the probability of picking a queen:

$$P(Q)=P(Q│H)P(H)+P(Q│D)P(D)+P(Q|C)P(C)+P(Q|S)P(S)$$

Basically, this is the same as weighted average.

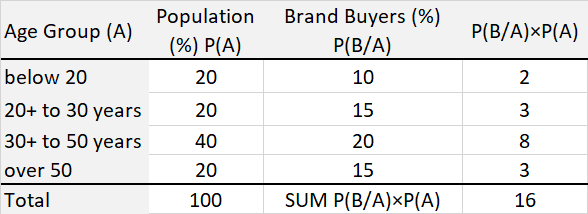
Example: As shown is Exhibit 34.6, the age profile of a target population (universe) is broken down into 4 groups: below 20, 20 to 30, 30 to 50 and over 50. The proportion of the population that falls in each group is 20%, 20%, 40% and 20% respectively, and the proportion of brand buyers in each is 10%, 15%, 20% and 15%. Based on this information, the proportion of brand buyers in the target population is 16%, as computed in Exhibit 34.6.