Sample Size — Population Proportions

When conducting quantitative research, it is common to focus on categorical parameters with discrete values, such as yes/no responses or a 5-point rating scale. These variables follow a binomial distribution, assuming that the population size is sufficiently large.

Typically, interest lies mainly in the proportions. For instance — What proportion of the population are aware of brand X? What proportion of consumers claim they will buy brand X? What proportion of consumers prefer formulation X over formulation Y? What proportion ‘agree’ or ‘strongly agree’ (top 2 boxes) about something?

These variables pertaining to the estimation of a proportion of the population, have two possible outcomes: “success” = 1, “fail” = 0. If the probability of success is p, then:

$$mean, \,µ = p; \,i.e. \,1 × p + 0 × (1-p)$$ $$variance, \,S^2;= p × (1-p)$$

Based on the Central Limit Theorem, for a sample size of n, the variance (σ²) of the distribution of sample proportion of successes can be approximated as: $$Variance, \,σ^2= \frac{p(1-p)}{n}$$

The upper bound (maximum value) of sample variance (σ²) is 0.25/n and the upper bound for σ (standard error) is 0.5/√n. This occurs when p=0.5.

Substituting the population variance (S²) in the sample size equation, the required sample size (n) for estimating proportion p̄ is:

$$ n=\frac {Z^2 × p(1-p)}{e^2},\; e = Z \sqrt {\frac {p(1-p)}{n}} $$

Where:

• p: is the probability for given response and varies from 0 to 1. It reflects the variability in the data. Note when p=1, (i.e., variance = 0) no sample is required.
• Z: is the standardized value associated with the level of confidence.
• e: is the margin of error.

The probability for which we require the largest sample size is p = 0.5. . Based on this “most conservative” value for p, and for a confidence interval of 95% (Z = 1.96), the required sample size (n) is determined as follows:

Z = 1.96 ≈ 2 for confidence level of 95%

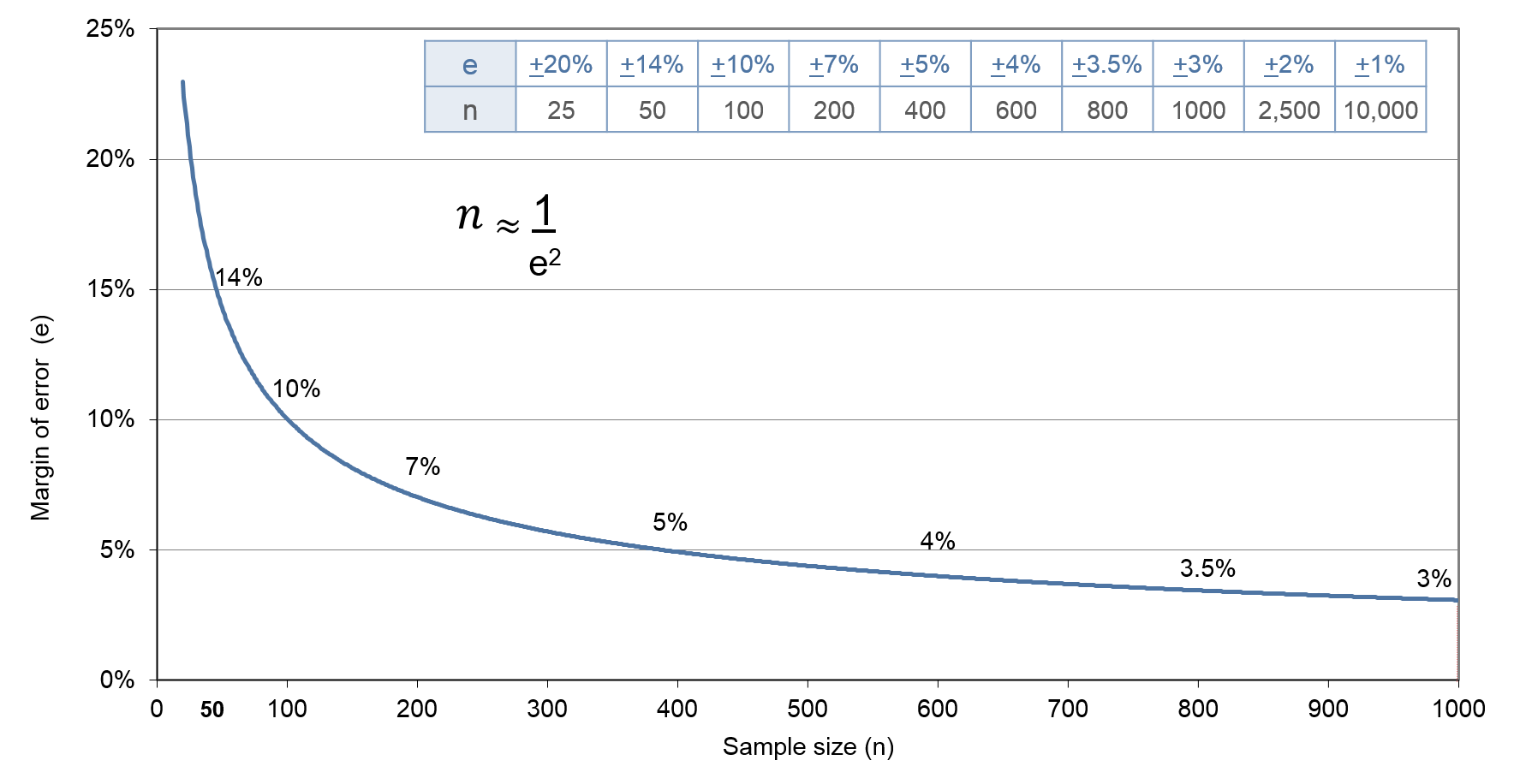
$$p = 0.5$$ $$n = \frac{Z^2p(1-p)}{e^2}≈\frac{2^2×0.5×(1-0.5)}{e^2}$$ $$n≈\frac{1}{e^2},\; e≈\frac{1}{\sqrt n}$$ $$n=\frac{0.96}{e^2},\; e=\frac{0.96}{\sqrt n}$$

Exhibit 34.3 shows how the largest required sample size n varies with the margin of error e. For example, if e = ± 5%, then for the confidence level of 95%, we require a sample of n = 400. Or 384 to be precise if Z (= 1.96) is not rounded off.

Note how the margin of error initially decreases sharply as the sample size, n, increases, and then more gradually. The improvement in accuracy after n=400, is relatively small compared to the increase in sample size.

Example: If 80 respondents out of a sample of 400 consumed a cola drink, we can conclude that 95 times out of 100 (confidence level of 95%), the estimate of the proportion of cola drinkers, over the specified time period, would lie between 16.1% and 23.9% (0.2 ± 0.039):

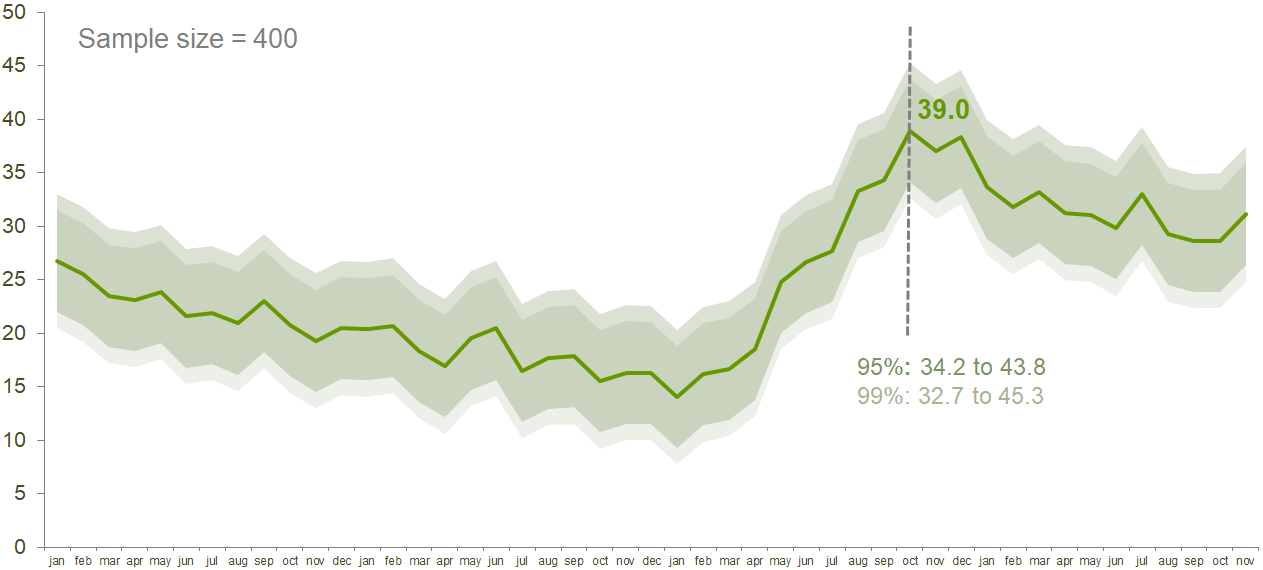
$$e = 1.96 × \sqrt{0.2(1-0.2)/400}=0.039 $$

Exhibit 34.4 tracks the results from a monthly study for some parameter along with the confidence interval for confidence levels of 95% (shaded dark) and 99%. The chart tells us that at the peak of 39.0, the confidence interval, taking Z=1.96 and p=0.39, was 34.2% to 43.8%.

The shading in Exhibit 34.4 is a helpful way to visualize the uncertainty in the estimates and to understand the statistical significance of the changes in the parameter. It reveals that while the trend over the years is clearly significant, much of the movement between consecutive months was not statistically significant, even at 95% confidence levels.

Finite Population Correction Factor

In the interest of saving costs, in cases where the universe size is not large, the sample size may be adjusted downwards. For medium size populations, the sample requirement is adjusted downwards using this formula:

$$ n_{adj} = \frac {n}{1+n/N} $$

For example, if N = 2000, e = 5% then

$$ n_{adj} = \frac {384}{1+384/1000} $$

Additionally, if it is known that the proportions are skewed (i.e., p is not close to 0.5) the sample may be further reduced.

For small universe populations, 100 for instance, it is advisable to take census instead of sample.