Sample Size — Continuous Parameters

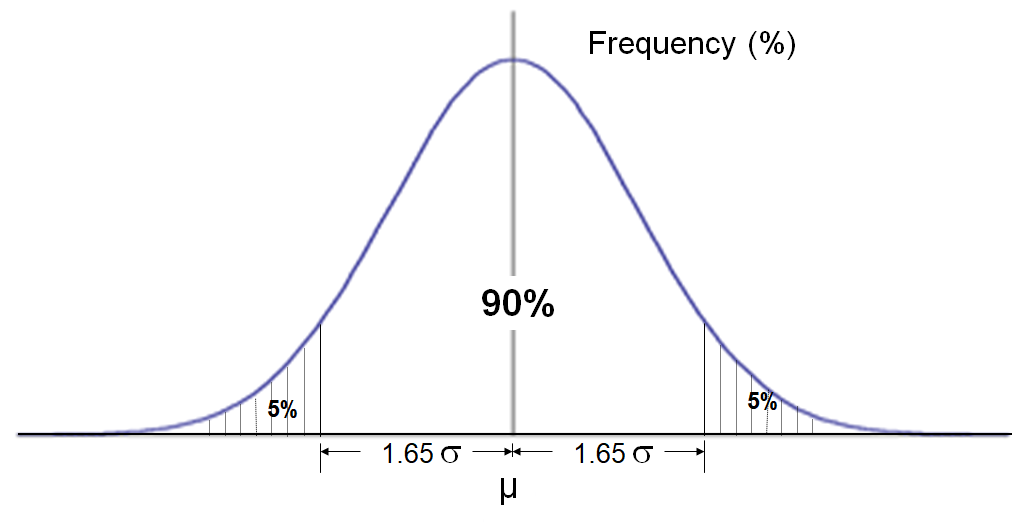
Exhibit 34.2  90% of the observations fall within a range of ±1.65 standard deviation from the mean.

When considering research programs like retail measurement, consumer panels, or TV audience measurement, where continuous variables such as sales, purchases, or viewership are tracked in a population, the determination of sample size is guided by the Central Limit Theorem (CLT).

As previously discussed, the sample size required to estimate a variable depends on the population variance, sampling design, and the desired level of precision, which is defined by two key statistics — confidence interval or margin of error and confidence level.

If the confidence level is set at 90% and the margin of error is denoted as e, then based on the normal distribution (refer to Exhibit 34.2): $$e = 1.65 σ$$

In general:

Where:

• e: margin of error
• Z: standardized value associated with the desired confidence level. For different confidence levels:
• 90% confidence level corresponds to Z = 1.65
• 95% confidence level corresponds to Z = 1.96
• 99% confidence level corresponds to Z = 2.58

Furthermore, according to the CLT the variance of the sampling distribution (σ²) is a function of the sample size (n), and the universe variance (S²): $$ σ^2 = \frac {S^2}{n} $$

Substituting for s ² :

If we express the margin of error as a proportion of the parameter value, denoted as e' = e/µ, and the relative sampling error as S' = RSE (relative sampling error) = S/µ, the above formulas can be rewritten as follows: $$\mathbf {n=\frac{Z^2S'^2}{e'^2}=\left(\frac{ZS'}{e'}\right)^2, \;\; e' = \frac {ZS'}{\sqrt n}}$$

Example 1: Consider a scenario where the standard deviation of sales for a category in provision shops is 80, and the average sales per store, μ, is approximately 200. We want to determine the required sample size to ensure that the sales estimates fall within ±6% of the true value with a confidence level of 90%. The calculation is as follows: $$n_{prov}=\left(\frac{ZS}{e}\right)^2=\left(\frac{1.65×80}{0.06 × 200}\right)^2=121$$

Take note that in order to half a sampling error we would need to quadruple the sampling size. For instance, if the sampling error was reduced to 3% (0.03), the required sample size will be 484.