Exhibit 36.2-2 Constant Returns to Scale (Linear) Model.
One of the most
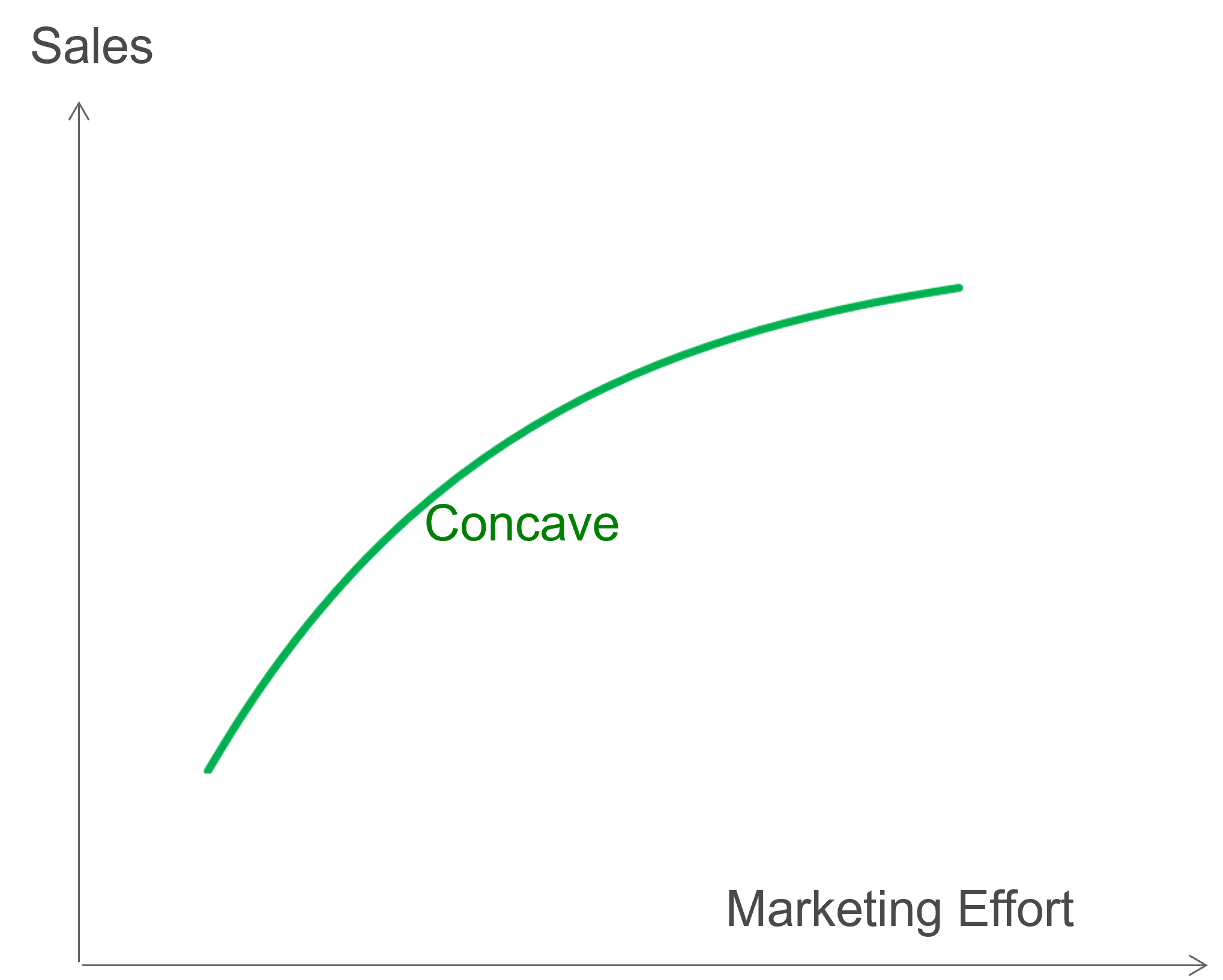
used forms in marketing mix modelling is the concave shape, which is characterized
by diminishing returns to scale as the marketing activity increases. This
aligns well with the expectation that as the intensity of discounts, displays
and advertising increases, the returns diminish.
The semilog (semi logarithmic) model is
an example of diminishing returns to scale function:
$$ S=α+βln(X) $$
Another functional form that meets the diminishing return to
scale requirement is the power model:
$$ S=e^α X^β, X>0\,and\,0<β<1.$$
Where S is sales, the dependent variable, and X is the independent variable representing the
marketing effort for the marketing mix element. α and β are model parameters.
The power model is also known as the constant elasticity
model due to its property that the power coefficient is the elasticity of
demand of the marketing mix variable X:
$$\epsilon=\frac{\delta S}{\delta X}×\frac{X}{S}=βe^α X^{β-1}×\frac{X}{e^α X^β}=β$$
The most widely used marketing mix model is a variation of
the power model, called the multiplicative model:
$$ S=e^α X_1^{β_1} X_2^{β_2} X_3^{β_3} ... X_j^{β_j}, $$
Where X1 to XJ are variables
representing the marketing effort for various marketing mix elements, and X1
to XJ > 0.
This nonlinear structural model can be transformed
into an estimation model that is linear in parameters by
taking logarithms on both sides. The advantage of this transformation, which is
shown below, is that the parameters of the original nonlinear model can be
estimated using linear-regression techniques.
$$ ln(S)=α+β_1ln(X_1)+β_2ln(X_2)+β_3ln(X_3) ... +β_jln(X_j) $$
The multiplicative form is widely used in marketing mix
models such as Nielsen’s Scan*Pro,
to evaluate promotions.