-
Promotion
Promotion
In-Store Promotion and Media
Types of Promotions
Trade Promotions
Consumer Promotions
Need to Rationalize Promotions
Promotion-Commotion-Demotion
Promotion Evaluation — Metrics
Basic Assessment of Sales Promotion
Market Modelling
Promotions Response Model
Model Validity — How Good is the Fit?
Watchouts and Guidelines
Store Level Modelling
Interpretation and Analysis
Discount Elasticity
Cannibalization
Displays and Cooperative Advertisement
Sales Decomposition and Due-To Analysis
What-If Analysis
- Price
- Promotion
- Marketing Education
- Is Marketing Education Fluffy and Weak?
- How to Choose the Right Marketing Simulator
- Self-Learners: Experiential Learning to Adapt to the New Age of Marketing
- Negotiation Skills Training for Retailers, Marketers, Trade Marketers and Category Managers
- Simulators becoming essential Training Platforms
- What they SHOULD TEACH at Business Schools
- Experiential Learning through Marketing Simulators
-
MarketingMind
Promotion
Promotion
In-Store Promotion and Media
Types of Promotions
Trade Promotions
Consumer Promotions
Need to Rationalize Promotions
Promotion-Commotion-Demotion
Promotion Evaluation — Metrics
Basic Assessment of Sales Promotion
Market Modelling
Promotions Response Model
Model Validity — How Good is the Fit?
Watchouts and Guidelines
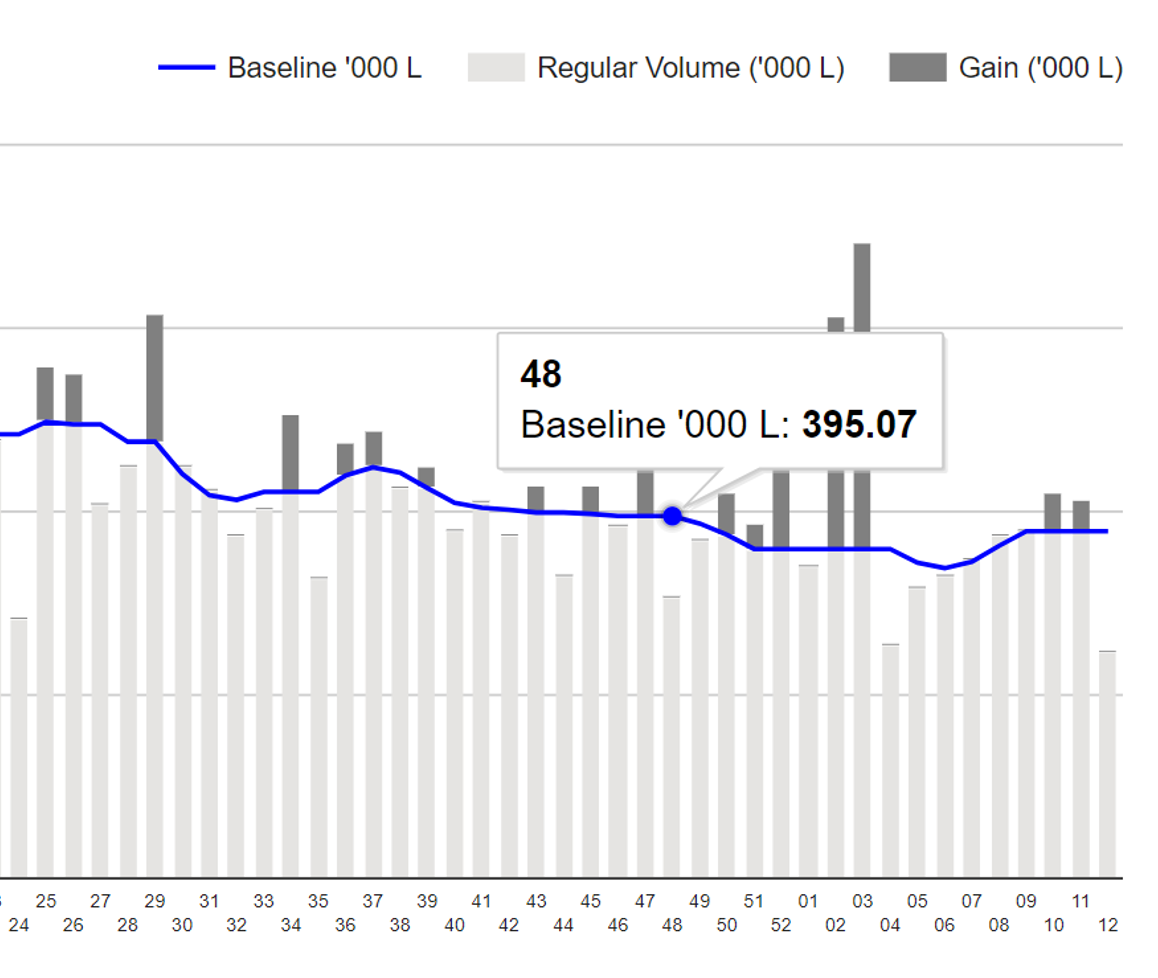
Store Level Modelling
Interpretation and Analysis
Discount Elasticity
Cannibalization
Displays and Cooperative Advertisement
Sales Decomposition and Due-To Analysis
What-If Analysis
- Price
- Promotion
- Marketing Education
- Is Marketing Education Fluffy and Weak?
- How to Choose the Right Marketing Simulator
- Self-Learners: Experiential Learning to Adapt to the New Age of Marketing
- Negotiation Skills Training for Retailers, Marketers, Trade Marketers and Category Managers
- Simulators becoming essential Training Platforms
- What they SHOULD TEACH at Business Schools
- Experiential Learning through Marketing Simulators
Promotions Response Model
The following multiplicative model is commonly used to model sales responsiveness to promotions:
$$ S_{ikt}=\left[\,\prod_{b=1}^{brands} \left\{\left(\frac{P_{bkt}}{\bar P_{bkt}}\right)^{β_{ibc}} \gamma_{1bic}^{D_{1bkt}} × \gamma_{2bic}^{D_{2bkt}} × \gamma_{3bic}^{D_{3bkt}}\right\}\,\right] $$ $$ \qquad × \left[\,\prod_{w=1}^{weeks} \nu_{icw}^{W_w} \,\right] × \left[\,\prod_{s=1}^{stores} α_{is}^{O_s} \,\right] × e^{\omega_{ikt}}$$Where:
Sikt : Sales for brand i in store k in week t.
Pbkt : Actual Price of brand j in store k in week t.
P̄bkt : Regular (median) Price of brand j in store k in week t.
D1bkt : Indicator for display. 1 if brand b in store k is displayed and not feature advertised in week t. Otherwise 0.
Note indicators (dummy variables) appear as exponents in a multiplicative model, otherwise sales will be zero when the indicator is off (value is zero).
D2bkt : Indicator for feature 1 if brand b in store k is featured advertised and not displayed in week t. Otherwise 0.
D3bkt : Indicator for display and feature. 1 if brand b in store k is featured advertised and displayed in week t. Otherwise 0.
Wkw : Indicator for week in store k (to capture seasonality). 1 if observation is in week w. Otherwise 0.
Ost : Indicator for store. 1 if observation is from store k. Otherwise 0
βibc : if b = i price (promotion) elasticity, otherwise if b ≠ i cross price (promotion) elasticity, in chain c. (The model has the attractive property that the power coefficients can be directly interpreted as elasticity. It is also referred to as the constant elasticity model).
γ1bic γ2bic γ3bic : if b = i Display/Feature Advertisement/Display + Feature Advertisement multiplier, otherwise if b ≠ i cross multiplier, in chain c. (A multiplier value of m means that brand sales increase m times when the brand’s promotion activity occurs).
νicw : Week w seasonal factor for brand i, in chain c.
αis : Store s’ intercept for brand i. This is the store’s baseline sales for brand i (i.e., regular sales for the brand when price equals the regular price and there are no promotion activities for any of the brands).
ωikt : Disturbance term for brand i in store k in week t.
This multiplicative structural model can be transformed into an estimation model that is linear in parameters by taking logarithms on both sides. The logarithmic transformation allows the model to be more easily estimated and interpreted.
This approach is adopted in popular models such as Nielsen’s Scan*Pro and IRI’s PromotionScan, which are widely used by FMCG manufacturers and retailers to evaluate their promotions and refine their promotion plans.
Aggregation of Models
In the promotions response model, discount elasticities, and promotional and seasonal lifts are assumed to be the same for stores in the same chain, and different for stores in different chains. In other words, parameters βibc, γ1bic, γ2bic, γ3bic, νicw are heterogeneous across chains and homogeneous within chains.
This store-level model with chain-specific parameters provides for greater accuracy, according to Foekens et al. (1994) who compared the forecast accuracy for store level, chain level and market level models.
While it is preferable to construct models with chain-specific parameters, due to data confidentiality clauses restricting the use of chain level data, the estimation of the parameters may be restricted to the aggregate channel or market level. This usually results in overestimation of the promotional effects.
From a business perspective, store level data is highly actionable for day-to-day tactical decisions — sales personnel and trade marketers need to know what promotions to run when and where. For manufacturer-to-retailer decisions and activities, key account, chain level data would seem most appropriate. On the other hand, marketing decisions and initiatives (manufacturer-to-consumers) need to be based on regional or country level data.
Dynamic Model
One limitation of the promotions response model is that it is static in nature. Causal factors are assumed to impact only the time periods when they occur, and carryover effects are not taken into consideration. Moreover, the market environment is assumed to be constant — model parameters remain fixed over the duration of the model.
Markets however do change. Post-promotional losses occur when consumers stockpile goods during promotional periods and then reduce their purchasing after the promotion ends. This phenomenon is often observed in markets after periods of intense festive promotions, such as during the holiday season or other special events.
Consumers’ response to price discounts and other causal factors fades if promotions are repeated too frequently. Frequent promotions also tend to induce an opportunistic behaviour — consumers lie in wait for the deals, resulting in the lowering of the base line. The parameters for price discount, promotion (e.g., display, co-op advertising) and baseline (i.e., store intercept) are therefore a function of historical levels of promotions.
The two ways that the dynamics of the marketplace can be captured are described in a paper by van Heerde et al. (2002). Firstly, the parameters may be set to vary while the structure of the model remains unchanged. In particular, functions are crafted to capture changes in price parameters (β), the promotion multipliers (γ) and the store intercept (α) arising from the magnitude, frequency and recency of promotional activities.
Alternatively dynamic promotion effects can be captured by incorporating leads and lags for promotion variables, into the original model.
Previous Next
Use the Search Bar to find content on MarketingMind.
Promotions Evaluation
Automated online solution for analysis of promotions.
Online Apps for training on Promotions
The Plannogrammer is an experiential learning facility for category managers, trade marketers, and retailers in consumer markets. Ideally suited for hybrid learning programmes, Plannogrammer imparts hands-on training in the planning and evaluation of promotions and merchandising.
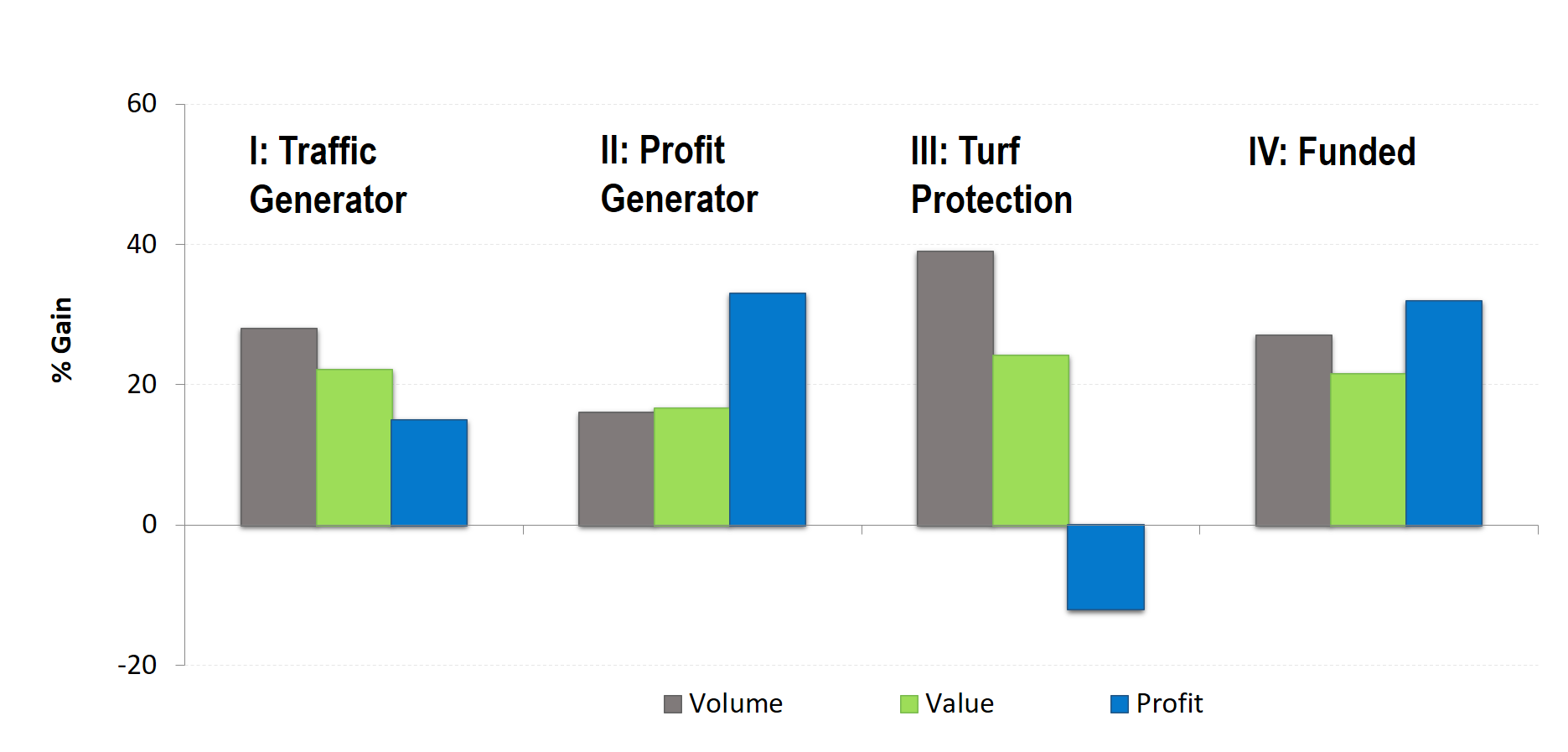
It supports a collection of simulation and analysis platforms such as Promotions and Space Planner for optimizing space and promotions, Plannogram for populating shelves and merchandising, a Due To Analysis dashboard that decomposes brand sales into the factors driving sales, and a Promotion Evaluator to evaluate the volume, value and profit impact of promotion plans.
Contact | Privacy Statement | Disclaimer: Opinions and views expressed on www.ashokcharan.com are the author’s personal views, and do not represent the official views of the National University of Singapore (NUS) or the NUS Business School | © Copyright 2013-2025 www.ashokcharan.com. All Rights Reserved.





