-
Marketing mix Modelling
Marketing mix Modelling
Sales Response Function
Linear
Concave
Convex
S-Curve
Interaction Effects
Competitive Effects and Market Share Models
Market Share Models
Dynamic Effects
Adstock
Adfactor
Leads and Lags
Parameter Functions
Long Term Effect (Advertising)
Baseline and Incremental Volume
Promotions Response Model
Model Validity — How Good is the Fit?
Watchouts and Guidelines
Interpretation and Analysis
Discount Elasticity
Cannibalization
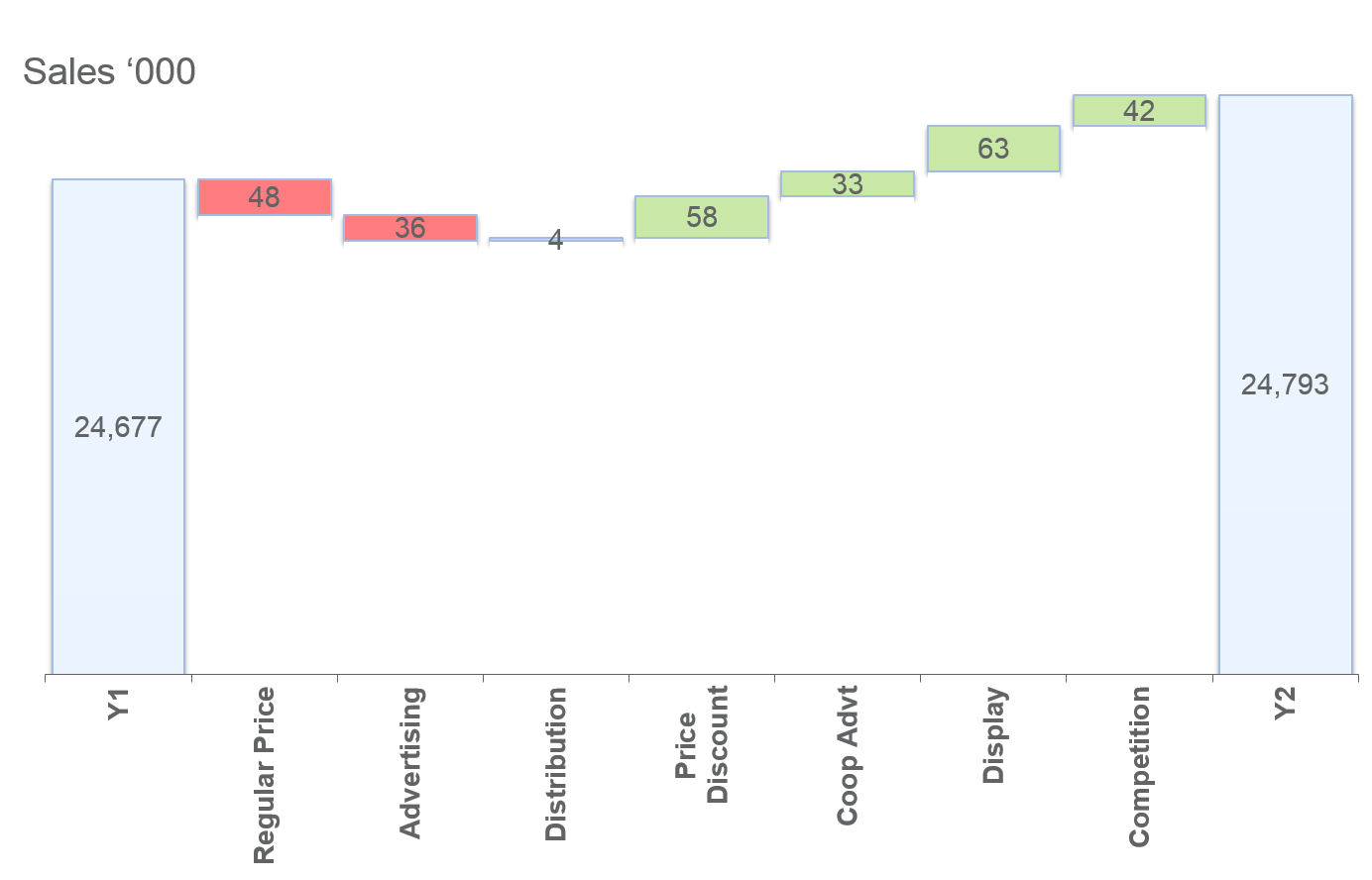
Sales Decomposition and Due-To Analysis
What-If Analysis
- Basic Statistics
- Sampling
- Marketing mix Modelling
- Marketing Education
- Is Marketing Education Fluffy and Weak?
- How to Choose the Right Marketing Simulator
- Self-Learners: Experiential Learning to Adapt to the New Age of Marketing
- Negotiation Skills Training for Retailers, Marketers, Trade Marketers and Category Managers
- Simulators becoming essential Training Platforms
- What they SHOULD TEACH at Business Schools
- Experiential Learning through Marketing Simulators
-
MarketingMind
Marketing mix Modelling
Marketing mix Modelling
Sales Response Function
Linear
Concave
Convex
S-Curve
Interaction Effects
Competitive Effects and Market Share Models
Market Share Models
Dynamic Effects
Adstock
Adfactor
Leads and Lags
Parameter Functions
Long Term Effect (Advertising)
Baseline and Incremental Volume
Promotions Response Model
Model Validity — How Good is the Fit?
Watchouts and Guidelines
Interpretation and Analysis
Discount Elasticity
Cannibalization
Sales Decomposition and Due-To Analysis
What-If Analysis
- Basic Statistics
- Sampling
- Marketing mix Modelling
- Marketing Education
- Is Marketing Education Fluffy and Weak?
- How to Choose the Right Marketing Simulator
- Self-Learners: Experiential Learning to Adapt to the New Age of Marketing
- Negotiation Skills Training for Retailers, Marketers, Trade Marketers and Category Managers
- Simulators becoming essential Training Platforms
- What they SHOULD TEACH at Business Schools
- Experiential Learning through Marketing Simulators
Marketing mix Modelling — Competitive Effects and Market Share Models
Markets operate within a competitive environment where consumer response to a product is influenced not only by its own attributes but also by the offerings of competitors. Understanding the competitive dynamics is crucial in marketing analysis and decision-making.
Take price for instance. When a product’s price is increased significantly, it is likely to lose business to competitors that offer similar products and target the same consumer segment. However, if all market players increase their prices by the same percentage, such as in the case of a hike in excise duties or rising raw material costs, the effect on sales tends to be less pronounced. For the majority of consumer goods, product categories as a whole are relatively inelastic to price adjustments. If individual brands increase prices, they tend to lose share. However, if the price of products like petroleum, milk, coffee, shampoo or cigarette increases across all brands in the category, the overall demand for those product categories is unlikely to plummet.
In summary, it is the relative value of a product that holds significance rather than its absolute value. This principle applies not only to price but also to other elements of the marketing mix.
The relative form of variables is often expressed in terms of an index or share — price index for relative price, share of market for sales, or share of voice (share of GRP or advertising expenditure) for advertising.
Cross elasticity is the construct that quantifies competitive effects. The cross elasticity of demand determines the responsiveness in the sales of a product when a change in marketing effort takes place in a competing product. When a product drops price, increases advertising, improves product quality or expands distribution, it cannibalizes competing products. The shift in business from one product to the other, on account of a change in marketing effort, is captured by the cross elasticity of demand.
Market Share Models
One approach to capturing competitive effects is via market share models, known also as attraction models. These models are based on the notion that marketing effort generates “attraction” for the brand, and that the brand’s market share is a function of its share of total marketing effort. This supposition is captured as follows:
$$ Market\,Share, \, M_b=\frac{S_b}{\sum_j^{brands} S_j}=\frac{A_b}{\sum_j^{brands} A_j},$$Where Mb and Sb are brand b’s market share and sales, and Ab is the effort expended over the brand’s marketing mix.
A commonly used form for Ab is the following multiplicative functional function:
$$A_b=e^{α_b}\prod_{k=1}^K X_{kb}^{β_{kb}}.e^{\delta_b}$$Where Xki > 0 are the K elements of the marketing mix.
The model as a whole is referred to as the Multiplicative Competitive Interaction (MCI) Model. The MCI model without taking cross-effects into consideration becomes:
$$ M_b=\frac{\left( e^{α_b}\prod_{k=1}^K X_{kb}^{β_{kb}} \right)e^{\delta_b}}{\sum_{j=1}^B \left( e^{α_j}\prod_{k=1}^K X_{kj}^{β_{kj}} \right) e^{\delta_j}},$$This nonlinear model can be transformed into a linear model by applying what is referred to as the log-centring transformation (Cooper & Nakanishi, 1988). After applying this transformation, the model takes the below form:
$$ ln \left(\frac{M_b}{\bar{M}}\right)=α_b^*+\sum_{k=1}^K β_k \,ln \left( \frac{X_{kb}}{\bar{X_k}} \right)+\delta_b^*,$$Where αb*=αb−x̄ and δb*=δb− 𝛿̄. Similarly, Xkb/X̄k can be expressed in log-centred format as Xkb* (M̄ and X̄k are the average market share and the average marketing effort for mix element k).
This model may be expanded to include terms that capture the cross effect between variables, i.e., βki ln(Xki/X̄) for i ≠ b.
MCI model is essentially the normalized form of the multiplicative model. Similarly, by specifying the attraction function (Ab) in terms of an exponential form (Ab = eαb eβ1bX1b eβ2bX2b eβ3bX3b ...), we derive what is referred to as the Multinomial Logit (MNL) model, which after applying the log centring transformation, takes the below form:
$$ ln \left(\frac{M_b}{\bar{M}}\right)=α_b^*+\sum_{k=1}^K β_k (X_{kb}-\bar{X_k})+\delta_b^*,$$Market share models offer several advantages. They effectively capture competitive effects. They meet logical consistency requirements — market shares for brands fall between 0 and 1, and the sum of all estimated market shares equals 1. Additionally, the response curves of market share models exhibit diminishing returns to scale at high levels of marketing activity. MCI models typically have a concave shape, while MNL models exhibit an S-shaped pattern.
One limitation of these models, however, is that they are static in nature. Marketing efforts are assumed to impact only the time periods when they occur, and the market environment is assumed to be static. These models do not account for potential carryover effects or changes in the market environment over time. Model parameters are assumed to remain fixed, which may not capture the dynamic nature of real-world marketing scenarios.
Previous Next
Use the Search Bar to find content on MarketingMind.
Contact | Privacy Statement | Disclaimer: Opinions and views expressed on www.ashokcharan.com are the author’s personal views, and do not represent the official views of the National University of Singapore (NUS) or the NUS Business School | © Copyright 2013-2025 www.ashokcharan.com. All Rights Reserved.