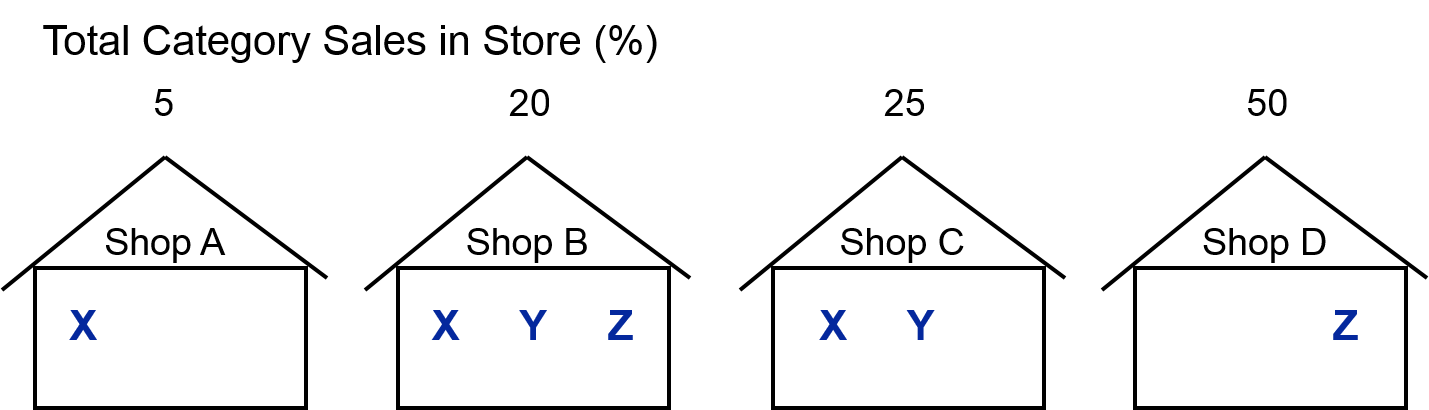-
Retail Tracking
Retail Tracking
The Nielsen Code
Applications of Retail Tracking
Where to Measure Sales?
Retail Measurement Services
Retail Universe
Retail Census
Sample Design — Retail Tracking
Data Collection — Retail Tracking
Data Processing — Retail Tracking
Data Projection — Retail Tracking
Analysis and Interpretation — Retail Tracking
Numeric and Weighted Distribution
In-Stock and Out-of-Stock Distribution
Coverage Analysis — Retail Tracking
Pipeline Effect
- Retail Tracking
- Sales and Distribution
- Retail Analytics
- Category Management
- Marketing Education
- Is Marketing Education Fluffy and Weak?
- How to Choose the Right Marketing Simulator
- Self-Learners: Experiential Learning to Adapt to the New Age of Marketing
- Negotiation Skills Training for Retailers, Marketers, Trade Marketers and Category Managers
- Simulators becoming essential Training Platforms
- What they SHOULD TEACH at Business Schools
- Experiential Learning through Marketing Simulators
-
MarketingMind
Retail Tracking
Retail Tracking
The Nielsen Code
Applications of Retail Tracking
Where to Measure Sales?
Retail Measurement Services
Retail Universe
Retail Census
Sample Design — Retail Tracking
Data Collection — Retail Tracking
Data Processing — Retail Tracking
Data Projection — Retail Tracking
Analysis and Interpretation — Retail Tracking
Numeric and Weighted Distribution
In-Stock and Out-of-Stock Distribution
Coverage Analysis — Retail Tracking
Pipeline Effect
- Retail Tracking
- Sales and Distribution
- Retail Analytics
- Category Management
- Marketing Education
- Is Marketing Education Fluffy and Weak?
- How to Choose the Right Marketing Simulator
- Self-Learners: Experiential Learning to Adapt to the New Age of Marketing
- Negotiation Skills Training for Retailers, Marketers, Trade Marketers and Category Managers
- Simulators becoming essential Training Platforms
- What they SHOULD TEACH at Business Schools
- Experiential Learning through Marketing Simulators
Numeric and Weighted Distribution
Exhibit 30.13 What is the numeric and weighted distribution of brands X, Y and Z? (Universe is shops A, B, C and D).
Distribution, the metric commonly used for tracking product availability, is usually measured in numeric and weighted terms. It may be weighted in either volume or value.
Numeric Distribution is the percentage of stores handling product.
Weighted Distribution is the percentage of stores handling product weighted by product category store sales. This is equal to share of category sales by handlers.
Let’s take the example presented in Exhibit 30.13 to understand the concepts of numeric distribution and weighted distribution.
In this example, Brand X is carried by three shops (handlers): A, B and C. The numeric distribution of Brand X is calculated by dividing the number of shops carrying the brand (which is 3) by the total number of available shops (which is 4), resulting in a numeric distribution of 75% (3 out of 4).
The weighted distribution of Brand X is determined by considering the total weight of the handlers (A, B and C) in terms of category sales. In the given example, the weighted distribution of Brand X is equal to 50%. This value is derived from adding up the category sales weights of each handler (5 + 20 + 25).
A brand’s weighted distribution can be defined as the brand’s handlers’ trade share of category sales. It corresponds to the handlers’ contribution to total category sales.
Unless otherwise specified, distribution is weighted in terms of category value sales. Defined as a percentage of where money is spent on the product category, it reflects the quality of distribution.
When comparing brand X and brand Z, it can be observed that brand X has a lower weighted distribution (50%) than its numeric distribution (75%). This suggests that the quality of brand X’s distribution is relatively weak. On the other hand, brand Z has a numeric distribution of 50% and a weighted distribution of 70%, indicating that it is handled by stores that make a more significant contribution to category sales.
By analysing these metrics, marketers and researchers can gain insights into the market presence and performance of a brand, considering both the number of shops carrying the brand and the sales weight associated with those shops.
Whereas weighting of stores on category sales is the norm, for certain categories, it is advisable to assign weights based on ACV (i.e., the sales value of all categories) or based on a collection of related categories. This practice is particularly beneficial for small, new, or growing categories that have a limited number of brands. For such categories, ACV weighted distribution is a better indicator of the quality of distribution.
Previous Next
Use the Search Bar to find content on MarketingMind.
Business Intelligence - Market and Trade
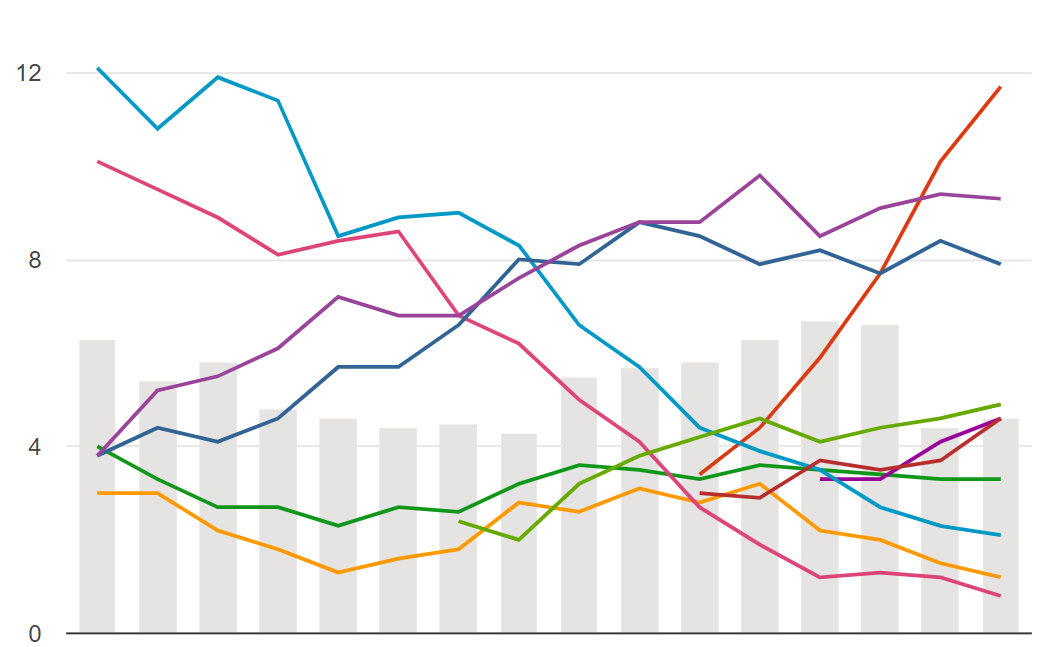
Suite of interactive, online dashboards that seamlessly integrate retail and consumer data sources in a manner that makes it easier to glean insights.
Scan Track
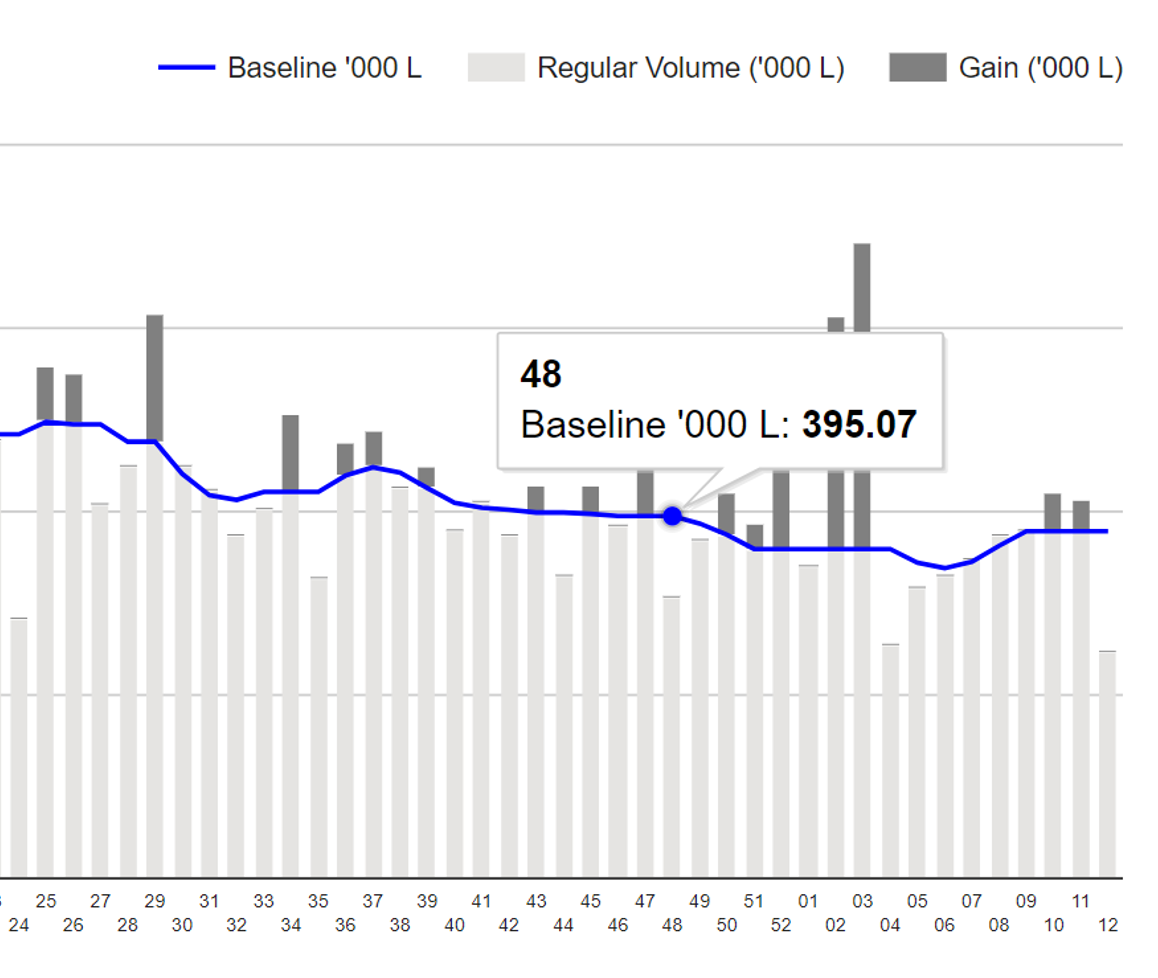
Suite of dashboards to visualize/analyse retail scan data.
Online Apps to train Retailers
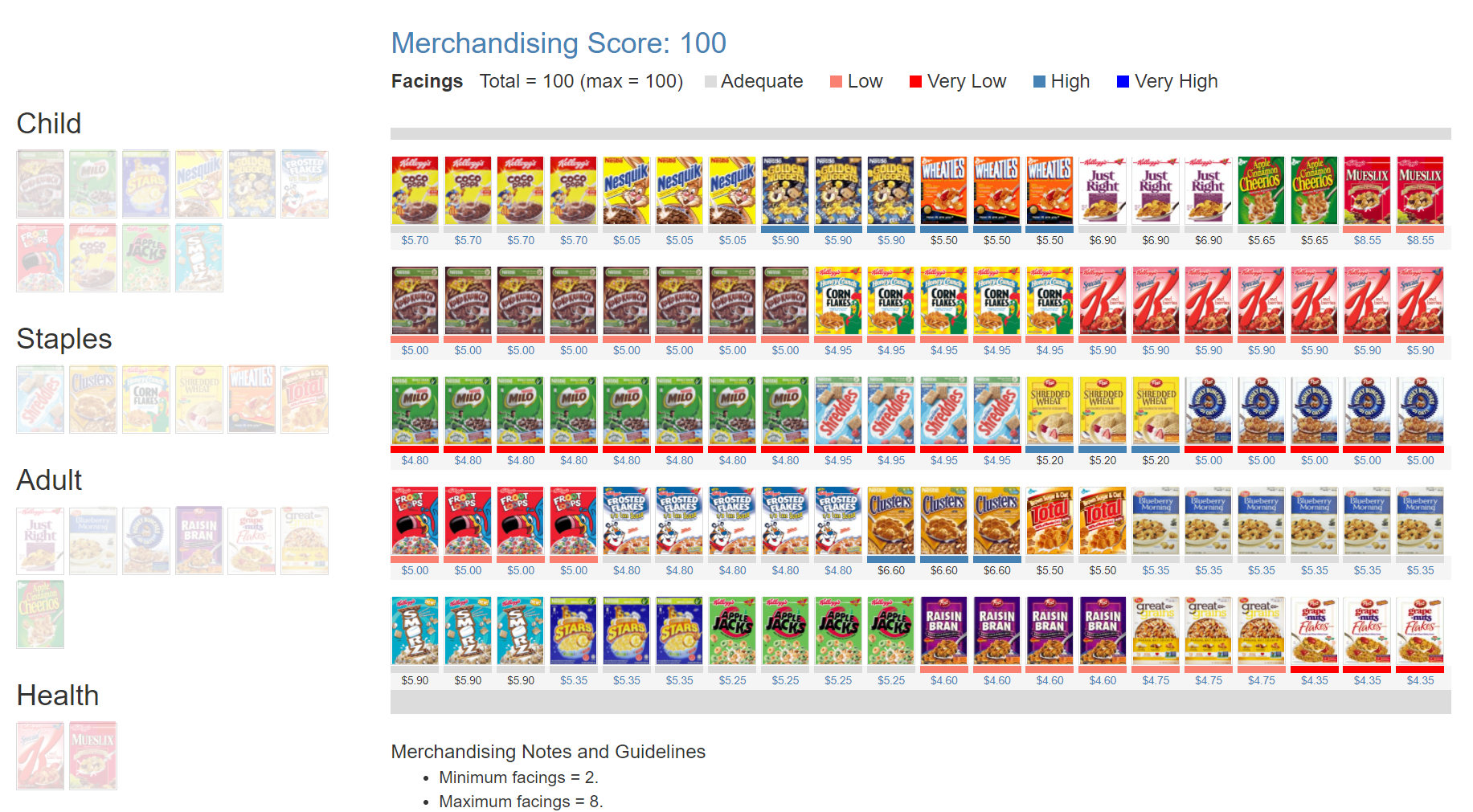
The Plannogrammer is an experiential learning facility for category managers, trade marketers, and retailers in consumer markets. Ideally suited for hybrid learning programmes, Plannogrammer imparts hands-on training in the planning and evaluation of promotions and merchandising.
It supports a collection of simulation and analysis platforms such as Promotions and Space Planner for optimizing space and promotions, Plannogram for populating shelves and merchandising, a Due To Analysis dashboard that decomposes brand sales into the factors driving sales, and a Promotion Evaluator to evaluate the volume, value and profit impact of promotion plans.
Contact | Privacy Statement | Disclaimer: Opinions and views expressed on www.ashokcharan.com are the author’s personal views, and do not represent the official views of the National University of Singapore (NUS) or the NUS Business School | © Copyright 2013-2025 www.ashokcharan.com. All Rights Reserved.